https://scontent-frt3-1.xx.fbcdn.net/.. ..f5e29989b99b13be8176a61b3&oe=56EFA2B2
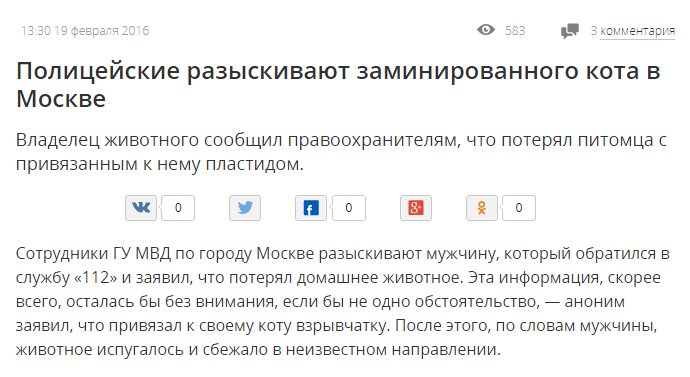
все правильно мордокнижка делает.
134 KB! ЯАНИС. ПРИХОДИ С ЯЙЦЕРАЗДЕЛИТЕЛЕМ В ВОСЕМЬ ДОЛЛАРОВ ЕГО ЭТА ЛЫСАЯ ТВАРЬ ИГРАЕТ ПРЕИМУЩЕСТВЕННО BREAKS ТОРМОЗА.
все правильно мордокнижка делает.
134 KB! ЯАНИС. ПРИХОДИ С ЯЙЦЕРАЗДЕЛИТЕЛЕМ В ВОСЕМЬ ДОЛЛАРОВ ЕГО ЭТА ЛЫСАЯ ТВАРЬ ИГРАЕТ ПРЕИМУЩЕСТВЕННО BREAKS ТОРМОЗА.
Рабочий роет котлован, гнёт об породу инструмент. Вот какая неудачная ситуация, думает, отковыривает кусок породы и даёт бригадиру:
— Вот об эту елду, Кузьмич, инструмент сломал, туды её в качель.
— Странно! Вроде должон инструмент всё молоть!
Бригадир приходит к инженеру и говорит:
— Михаил Максимыч, мы тут при ройке котлована, об эту руду инструмент погнули. Примите меры, а то не можем инструментом рисковать.
— Странно, по спецификациям инструмент должен быть крепче!
Приносит инженер кусок породы физику и говорит:
— Посмотрите, Геннадий Саввович, что это за руда крепче стального сплава №ххх с алмазным покрытием.
— Странно! Судя по пористой структуре эта порода должна быть очень хрупкой!
Подходит физик к теоретику:
— Герман, а как это может фрактальная сводчатая микроструктура оксида металла сопровождаться сильно плотным электронным распределением электронов связи типа так, что атомы связываются крепче чем в кристалле алмаза?
— Странно! В работе N в семидесятых было показано, что блоховское решение для случая квазипериодической решётки, к которой NN свёл фрактальную структуру, реализует квазинепрерывную плотность состояний Zagge для тетраэдрических решёток!
Идёт теоретик к математику спрашивает:
— Слушай, Саня, а разве учёт членов выше третьего порядка может привести к появлению серии решений уравнения NNN в случае NNNN с нелинейной правой частью?
— Да, там есть такой вариант, если асимптотически третье слагаемое стремится к нулю на бесконечности не хуже чем минус вторая степень.
— Ааа, Гена как раз и говорил, что там дисперсия пор нетипично узкая. Понятно, спасибо.
Ловит теоретик физика в коридоре и объясняет:
— Если дисперсия пор невелика, то фрактальная пористая структура сводится к тетраэдрической сингонии квазикристалла, а не к гексагональной.
— Ааа, то есть мы тут имеем дело с губками первого рода. Понятно, пустим проект алмазного покрытия NNNNN, они достаточно крепкие должны быть.
Рассказывает физик инженеру:
— Мы тут доработали алмазное покрытие, должно теперь эту породу брать. Вот вам несколько опытных образцов, опробуйте.
— А что это за руда была?
— Да там поры мелкие слишком.
— Ааа, то есть просто своды крепче. Понятно, ну пока этим подолбим.
Отдаёт инженер бригадиру новый инструмент:
— Иван Кузьмич, вот новый инструмент, его лучше покрыли.
— Ааа, так там просто покрытие плохое было! Спасибо, а то я за сохранность инструмента не могу отвечать, когда его чёрти–как покрывают.
Даёт бригадир рабочему инструмент:
— Держи, на этот инструмент покрышки не скупили.
— Ааа, так там просто жиды полировку пожалели! Эх, развалили страну
— Вот об эту елду, Кузьмич, инструмент сломал, туды её в качель.
— Странно! Вроде должон инструмент всё молоть!
Бригадир приходит к инженеру и говорит:
— Михаил Максимыч, мы тут при ройке котлована, об эту руду инструмент погнули. Примите меры, а то не можем инструментом рисковать.
— Странно, по спецификациям инструмент должен быть крепче!
Приносит инженер кусок породы физику и говорит:
— Посмотрите, Геннадий Саввович, что это за руда крепче стального сплава №ххх с алмазным покрытием.
— Странно! Судя по пористой структуре эта порода должна быть очень хрупкой!
Подходит физик к теоретику:
— Герман, а как это может фрактальная сводчатая микроструктура оксида металла сопровождаться сильно плотным электронным распределением электронов связи типа так, что атомы связываются крепче чем в кристалле алмаза?
— Странно! В работе N в семидесятых было показано, что блоховское решение для случая квазипериодической решётки, к которой NN свёл фрактальную структуру, реализует квазинепрерывную плотность состояний Zagge для тетраэдрических решёток!
Идёт теоретик к математику спрашивает:
— Слушай, Саня, а разве учёт членов выше третьего порядка может привести к появлению серии решений уравнения NNN в случае NNNN с нелинейной правой частью?
— Да, там есть такой вариант, если асимптотически третье слагаемое стремится к нулю на бесконечности не хуже чем минус вторая степень.
— Ааа, Гена как раз и говорил, что там дисперсия пор нетипично узкая. Понятно, спасибо.
Ловит теоретик физика в коридоре и объясняет:
— Если дисперсия пор невелика, то фрактальная пористая структура сводится к тетраэдрической сингонии квазикристалла, а не к гексагональной.
— Ааа, то есть мы тут имеем дело с губками первого рода. Понятно, пустим проект алмазного покрытия NNNNN, они достаточно крепкие должны быть.
Рассказывает физик инженеру:
— Мы тут доработали алмазное покрытие, должно теперь эту породу брать. Вот вам несколько опытных образцов, опробуйте.
— А что это за руда была?
— Да там поры мелкие слишком.
— Ааа, то есть просто своды крепче. Понятно, ну пока этим подолбим.
Отдаёт инженер бригадиру новый инструмент:
— Иван Кузьмич, вот новый инструмент, его лучше покрыли.
— Ааа, так там просто покрытие плохое было! Спасибо, а то я за сохранность инструмента не могу отвечать, когда его чёрти–как покрывают.
Даёт бригадир рабочему инструмент:
— Держи, на этот инструмент покрышки не скупили.
— Ааа, так там просто жиды полировку пожалели! Эх, развалили страну
Сходи из спальне за чайком, ХЗ кто...
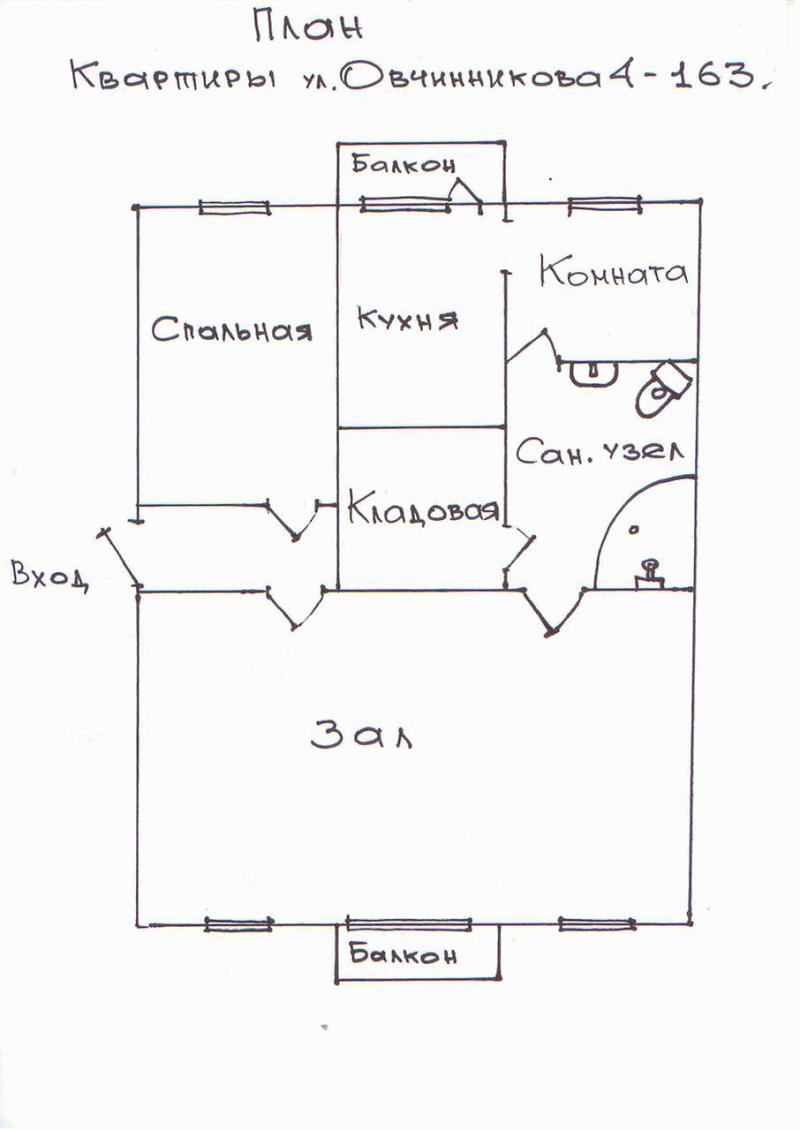
Только там дядя Коля сдрёт, но ты не обращай внимания.
Подробносте, для желающих:
http://vladivostok.farpost.ru/otlichnaja-kvartira-na-stoletii-22329031.html

Только там дядя Коля сдрёт, но ты не обращай внимания.
Подробносте, для желающих:
http://vladivostok.farpost.ru/otlichnaja-kvartira-na-stoletii-22329031.html